How to Calculate Net Present Value (NPV)?
Net present value is a summation of a series of future cash flows expressed in present values. It is a tool used to assess the viability of an investment done during a period. Net present value takes into consideration both, investments done and revenues generated during a period of time. If the NPV is positive (i.e. greater than 0), the project is viable and if it is negative (i.e. less than 0), then it is not viable.
NPV is of paramount importance because money as a commodity has a time value. In an inflationary economy the purchasing power of money gets eroded with the passage of time. Hence, every individual prefers money in hand today for consumption/investment rather than, at a later date. A rupee employed today can be spent or invested more effectively than a rupee employed later.
Net Present value for Capital Budgeting
Most of business houses come across various investment options and they have to choose between them diligently. One of the tools used, is the net present value to evaluate the profitability of the projects. Most of the projects involve several investments and receipts during the period of the project. All these values are summed up and converted in present values for comparison between projects.
The NPV can be calculated effectively only if the discount rate is applied correctly. It is the rate which is used to discount the cash flows. This rate is the market discount rate for businesses of like market risks and keeps in view the future expectations. The formula used to calculate the NPV is :
NPV = SUM {(Amount of future cash flows) / (1 + i ) t } - Initial investment
Where i = discount rate and t = no. of years.
This concept can be explained better with an example:
A business house got a proposal for investment of Rs.10000/-. The house wants a minimum 10% return to go ahead with the proposal. The project will last for 3 years. The profit earned in each year will be:
Year 1 – Rs.3000/-
Year 2 – Rs.4300/-
Year 3 – Rs.5000/-
Will the business house take up the project?
Solution A :
For an ordinary being, the returns are 3000+4300+5000 = 12300. This is seemingly profitable compared to the expected return on investment on Rs.10000/-.
Solution B: NPV Method
In order to compute the present value of 3 years cash flows, we will find the present value of each cash flow. The present value factor can be seen from the Present Value Table. The Present Value Table gives the present value of Rs.1/- , when it is discounted by the desired rate of return for n years.
Present Value of Cash Flows
|
Year
|
Cash Flows
|
PV Factor at 10%
|
Present value (2*3)
|
|
1
|
3000
|
0.909
|
2727
|
|
2
|
4300
|
0.826
|
3551.8
|
|
3
|
5000
|
0.751
|
3755
|
|
|
|
|
10033.8
|
NPV = 10033.8 - 10000 = 33.8
Thereby this project gets a go ahead as the NPV is positive i.e greater than 0.
As seen in the above example, the initial investments are netted against the future cash inflows to arrive at the NPV. This is because, there is an initial cash outflow and no income is generated for the first year. However, in case of annuities/home loans, etc NPV is calculated by only discounting the series of payments/ income.
Net Present value for Annuity
When payments are received at the end of the month by way of pensions, payments made for loan mortgages, etc., the formula used is
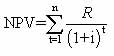
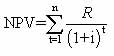
The inflow is discounted by the interest rate, the time period starts at 1 and ends at n the last period at which the annuity receipt or payment is due.
Net Present value for Annuity due
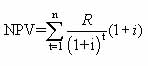
When payments are made at the start of the month, like lease or rental payments, the formula used is
Each receipt/payment is discounted at the interest rate i for the time period t-1.
Contributed By: Aruna Sharma |
|
Mrs. Sharma holds a Masters in Financial Management from University of Mumbai. She has graduated from the University of Mumbai. | |


p